Zahlensysteme
Wir Menschen rechnen schon immer im Dezimalsystem. 10 + 40 = 50, positive wie negative Zahlen, Hunderter Stellen, Tausender Stellen, doch, dass ist bei weitem nicht jedes Zahlensystem das existiert. Das Dezimalsystem ist die Basis 10, so gibt es beispielsweise noch hexadezimal zur Basis 16 oder das Oktalsystem zur Basis 8. Wichtig für das folgende wird vorerst nur das Binärsystem zur Basis 2 sein. In diesem gibt es lediglich zwei Zustände, an und aus, oder auch 1 und 0. Boolsche Logik basiert nun darauf, diese Zustände mit Gattern zu Verarbeiten und mit vielen anderen Gattern ein System an Funktionalität zu erzeugen.
Logische Verknüpfungen
| a | b | Konjunktion („und“) A ∧ B | Disjunktion („oder“) A ∨ B | Implikation A ⇒ B | Äquivalenz A ⇔ B | Negation von A ¬A |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 |
Oder in anderen Worten:
- Konjunktion ist genau dann wahr, wenn A und B wahr sind
- Disjunktion ist genau dann falsch, wenn A und B falsch sind
- Implikation ist genau dann falsch, wenn A wahr und B falsch ist
- Äquivalenz ist genau dann wahr, wenn A und B gleich sind
- Negation ist genau dann falsch, wenn A wahr ist
Diese Verknüpfungen sind schon unsere Gatter, Konjunktion – AND, Disjunktion – OR, Negation – NOT. Diese drei haben eine ganz bestimmte Art und Weise dargestellt zu werden.
AND-Gate
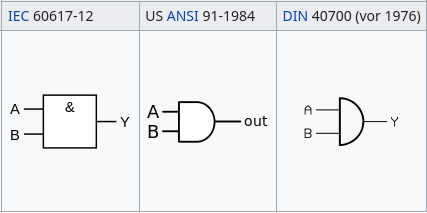
OR-Gate
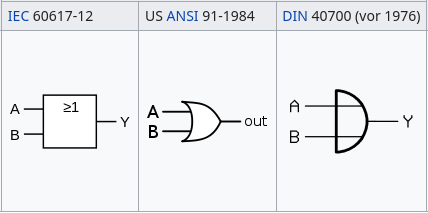
NOT-Gate
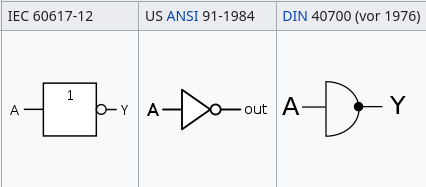
Erste Eigene Gatter
NAND und NOR
Mit diesem Wissen können wir schon unsere ersten Gatter erstellen. Fangen wir an mit einer simplen Fusion von einem AND und einem NOT Gate. Beide zusammen ergeben ein sogenanntes NAND-Gate, was folgendermaßen aussieht.
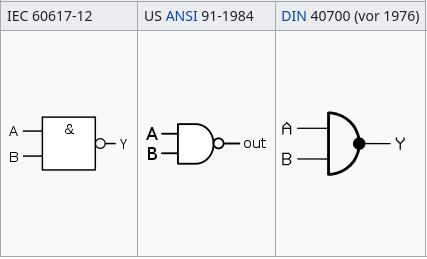
Aufmerksamen lesern ist sicherlich aufgefallen, dass dieses Gatter einfach ein AND-Gate mit einem Punkt an der Vorderseite ist. So negiert man irgendwelche Gatter, so kann man einfach ein Punkt an den jeweilig negierten in- oder Output setzen. Die simulierten gezeigten Bilder sind aus dem Programm Logic Data Sim, mit dem man wundervoll rumexperimentieren und ausprobieren kann.
Ein NAND-Gate sieht formell auf dem Blatt papier zum Beispiel folgendermaßen aus:
¬(A ∧ B)
Und umgesetzt folgendermaßen:

Die Wahrheitstabelle sehe jetzt folgendermaßen aus:
| A | B | Out |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOT-OR, also NOR ist gleichermaßen mit OR und NOT Implementierbar.
XOR and XNOR
Das X for dem OR steht in beiden Fällen für „exclusive“, also exclusive or und exclusive not or.
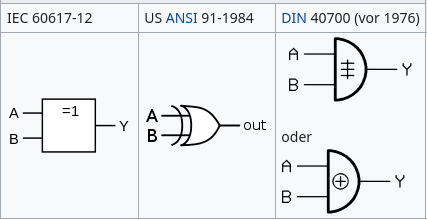
Das exklusive Oder steht dabei für jeden Werte, die nicht gleich sind, also die Umgekehrte Äquivalenz. Die Implementation dieses ist garnicht so einfach wie die des NAND oder NOR Gatters. Zuerst werfen wir mal einen Blick auf die Wahrheitstabelle.
| A | B | Out |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Aus einer Wahrheitstabelle sind per Disjunktiver Normalform und Konjunktiver Normalform logische Verknüpfungen erstellbar. Diese können dann per Karnaugh-Veitsch Diagram vereinfacht werden. Dies ist sehr theoretisch und wird in einer späteren Episode besprochen. Hier nutzen wir jetzt die Implementation von Wikipedia.
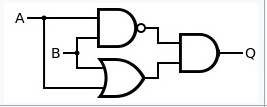
Der Input A führt in ein NAND und ein OR, das B ebenfalls. Beide Outputs dann wieder in eine AND, wessen der Output ist. Doch um das ganze Simulierend zu Implementieren müssen wir erstmal ein OR Implementieren, da dieses nicht standardmäßig dazu gehört. Um dieses zu erstellen benötigen wir drei NAND-Gates.
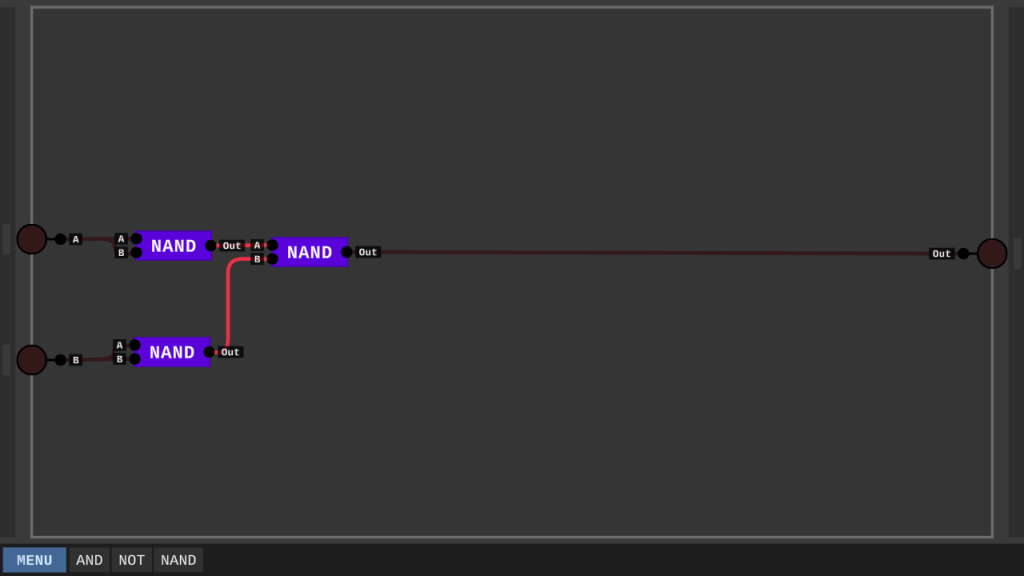
Mit dem neuen OR-Gate können wir nun das XOR erstellen und direkt die Wahrheitstabelle durchprüfen.
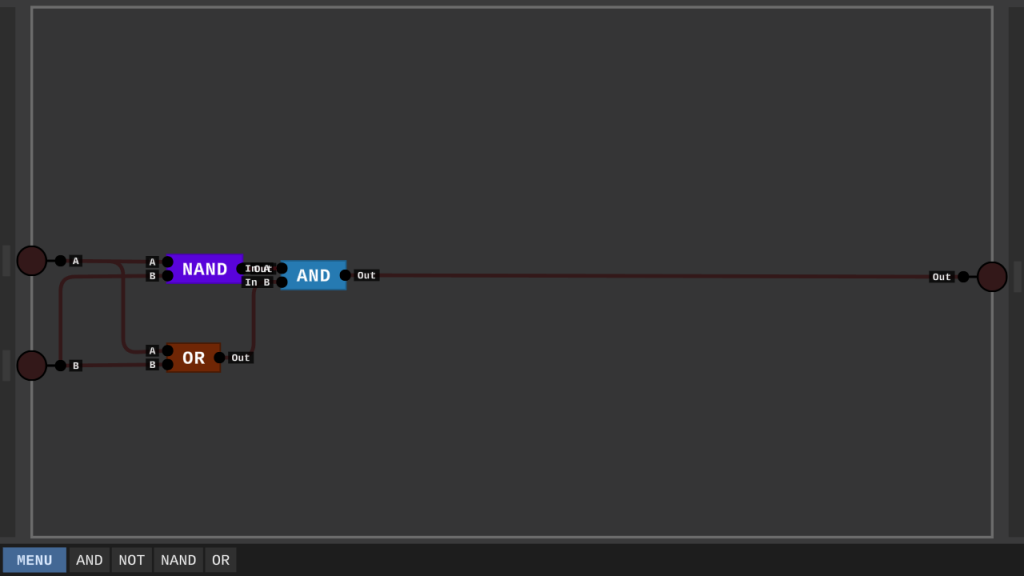
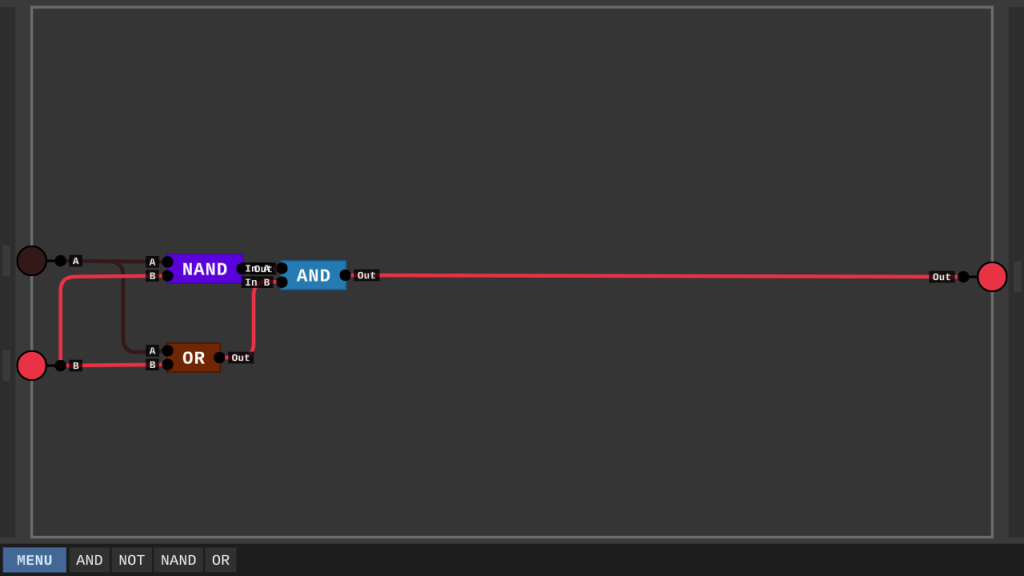
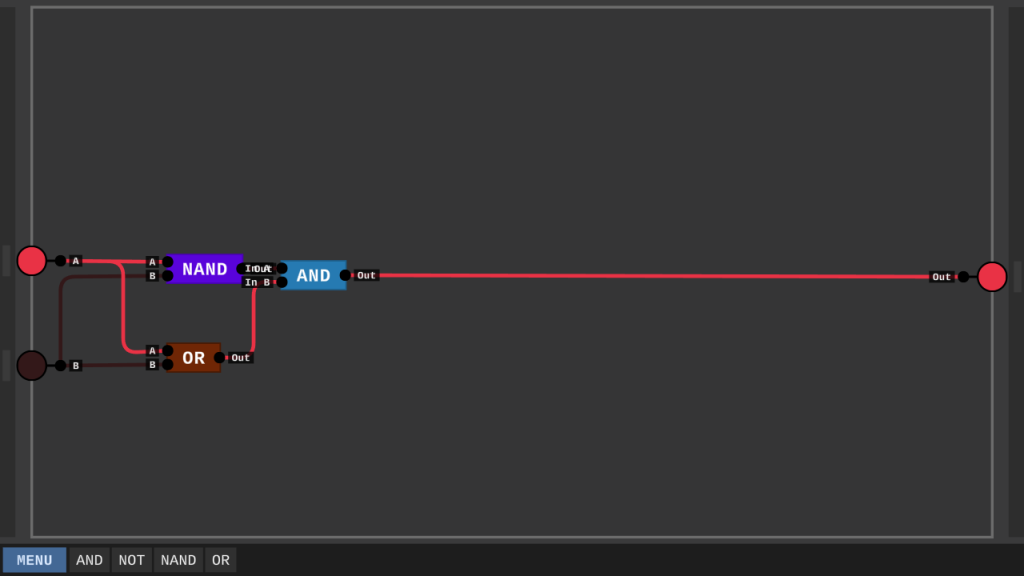
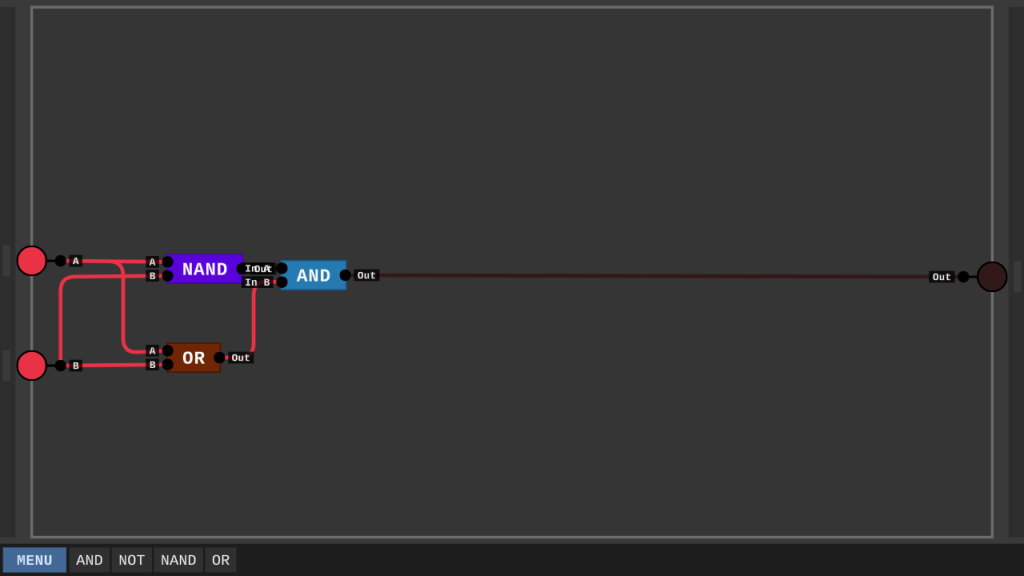
Binärzahlen
Erstmal müssen wir die Darstellung eines Bytes verstehen. Ein Byte repräsentiert eine Folge von 8 Bits, die jeweils 1 und 0 darstellen, also zum Beispiel 01101110. Elektrotechnisch steht eine eins für eine bestimmten Spannung in einem Transistor und eine Null für einen nahe null Wert. Rückwärts kann man die Stellen aufsteigend betrachten. Die erste Stelle von hinten hat den Kontrastwert 1, dieser ist hier auf 0 gestellt, also aus. Der nächste 2, dieser ist an, also notieren wir uns die zwei. Die Kontrastwerte werden dabei immer gedoppelt, also ist die nächste Stelle 4, an. Dies lässt sich folgendermaßen darstellen:
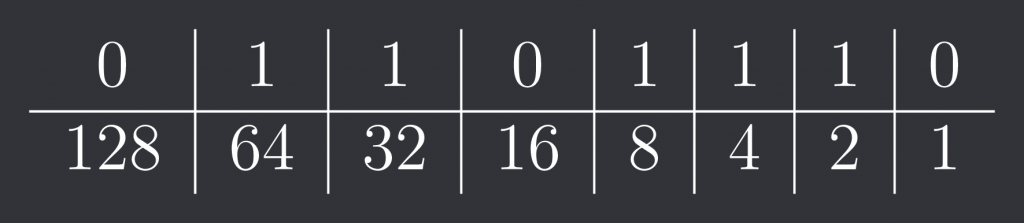
Summieren können wir nun die Werte die als „an“, also mit einer 1 markiert sind. 2+4+8+32+64 = 110. Um nun Binärzahlen zu addieren, brauchen wir folgende Formelle regeln:

Wenn wir nun also die Werte 100110 und 111010 miteinander addieren wollen, dann sieht dies folgendermaßen aus:

Hier kann man die Regeln gut Widerspiegeln, die zwei Blauen Einsen, ergeben eine die Rote 10 und die drei gelben Einsen ergeben die grüne 11. Dies kann man natürlich auch mit logischen Gattern implementieren
Halbaddierer
Ein Halbaddierer addiert zwei einzelne Bits indem man genau diese Regeln anwendet. Dabei gibt es Input A und B und Output S und Cout. Der Output S ist dabei die entstandene Summe und Cout ist der sogenannte „Carry-Out“, oder auf Deutsch, übertrag. Die Wahrheitstabelle für einen Halbaddierer sieht dann so aus:
Über das kostenlose Tool Logic Friday können wir nun von dieser Wahrheitstabelle zu Logischen Gates kommen. Über File – New – New Truth Table können wir eine Neue Tabelle erstellen.
Durch doppeltes Anklicken der Ergebnisse können die Werte abgeändert werden.
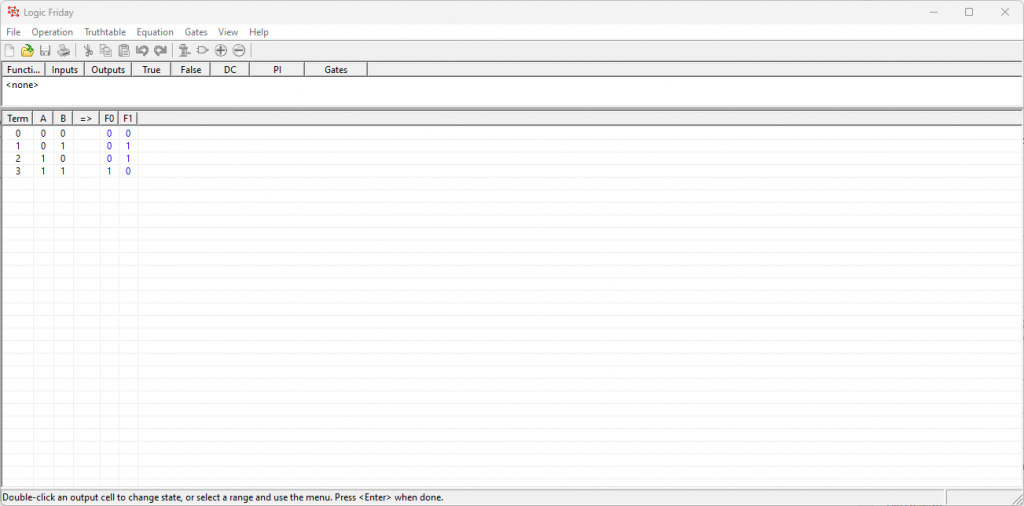
Wenn wir nun mit einem Rechtsklick und einem Klick auf „Submit“ die Wahrheitstabelle bestätigen, ist diese nun im System. Über dem Reiter Operationen und dem Button „Map to Gates“ können wir uns nun das ganze mit Gates plotten lassen. Nun könne wir alle uns verfügbaren Gates auswählen (MUX haben wir noch nicht implementiert)
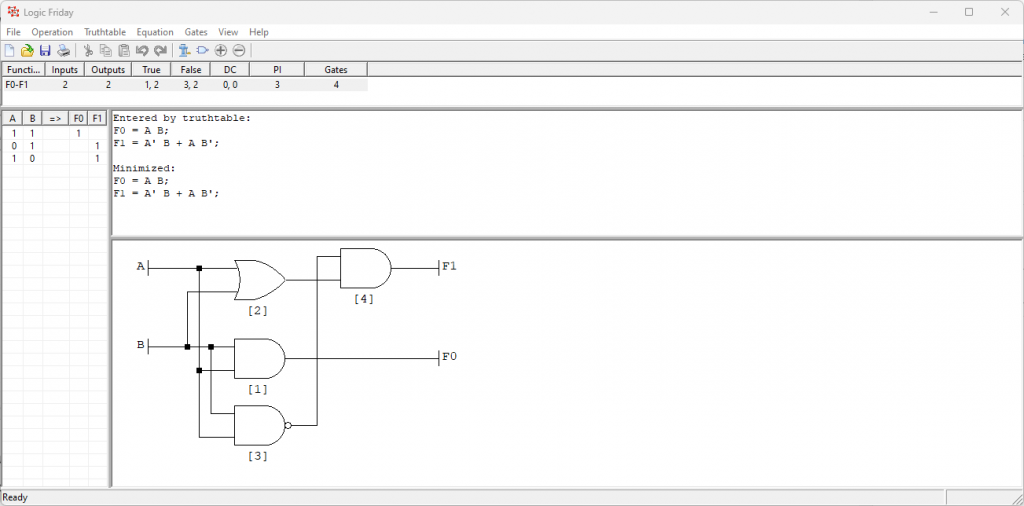
Diese Darstellung können wir nun mit dem Digital Logic Sim simulieren.
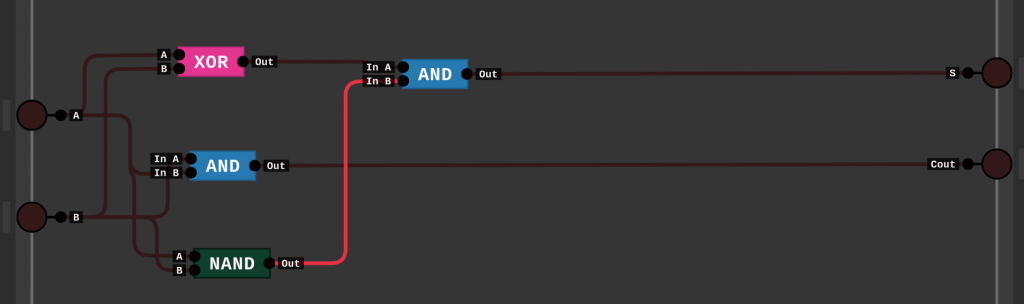

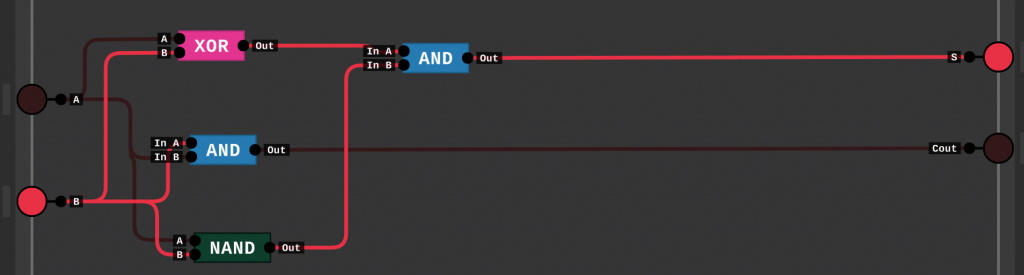
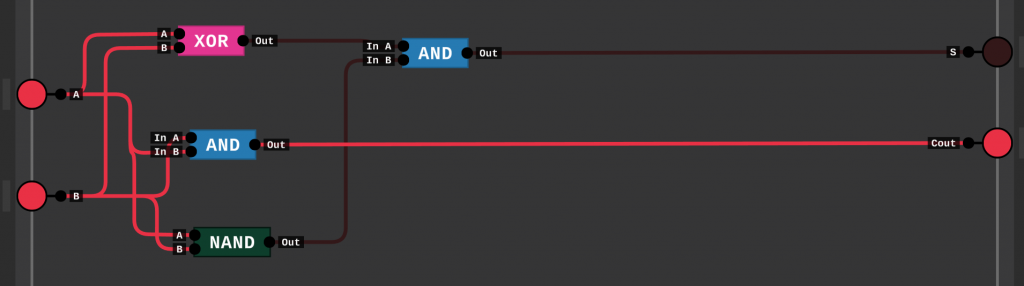
Volladdierer
Ein Volladdierer unterscheidet sich insofern von einem Halbaddierer, dass der Volladdierer drei Eingänge hat (A,B und Cin). Eine Wahrheitstabelle für diesen sieht so aus:
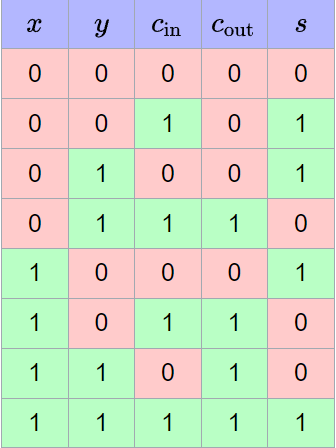
Um dies nun zu Implementieren, können wir hierbei zwei Halbaddierer und ein OR-Gate.
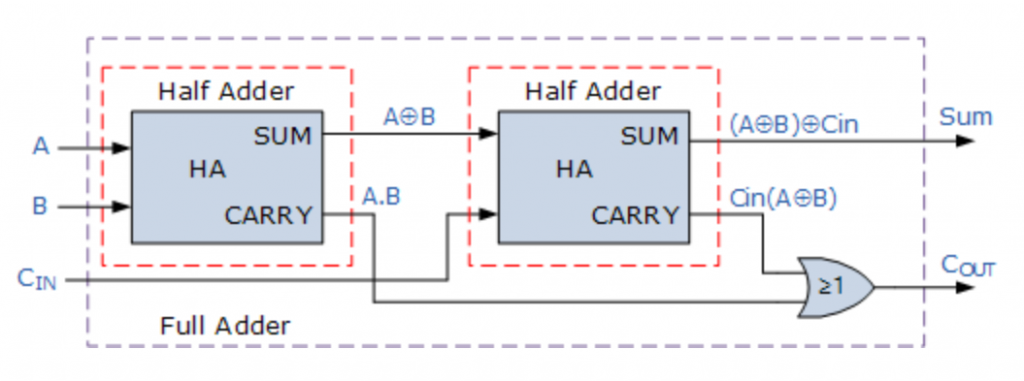
Bewiesen wird die Funktionalität der Implementierung hier nur an drei Beispielen.



Addierwerk
Das Addierwerk ist die Zusammensetzung dieser Volladdierer zu einem Netzwerk, sodass größere Zahlen miteinander addiert werden können. Dieses könnte man als die Hauptkomponente einer CPU betiteln, da alle vier Grundrechenarten auf Addition zurückführbar sind.
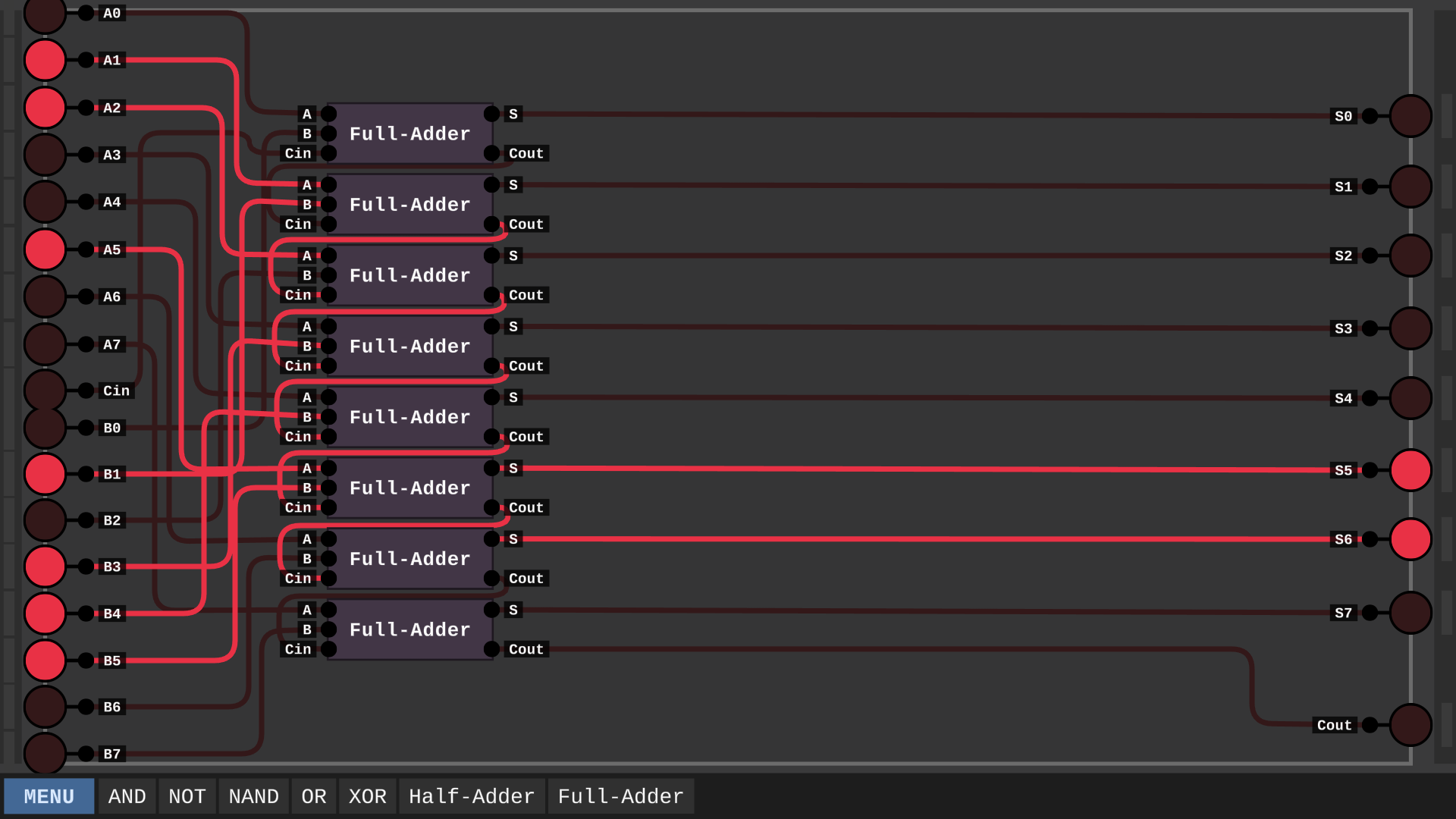
Um nun also 2 Bytes miteinander Addieren zu können, setzen wir 8 Volladdierer hintereinander.
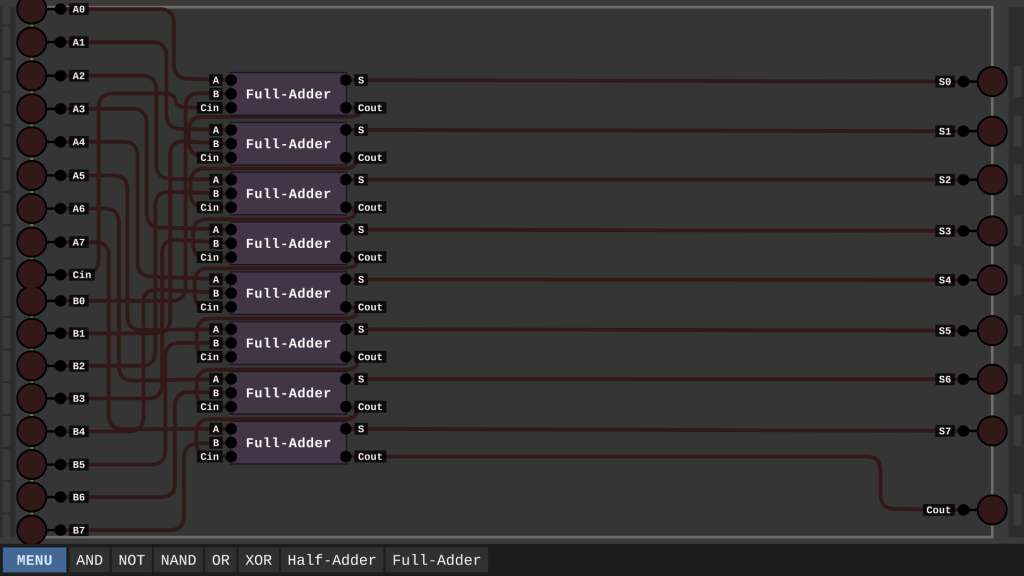
Diese Verbindung sieht ziemlich chaotisch aus, aber so schwer ist es gar nicht. Die A0-A7 gehen in die A in und B0-B7 in die B in. Der Cin geht in den ersten Cin des Volladdierers und dessen Cout in den nächsten Cin. Wenn wir nun unser Additions Beispiel von 100110 und 010111 testen, kommt dabei das richtige Ergebnis raus.
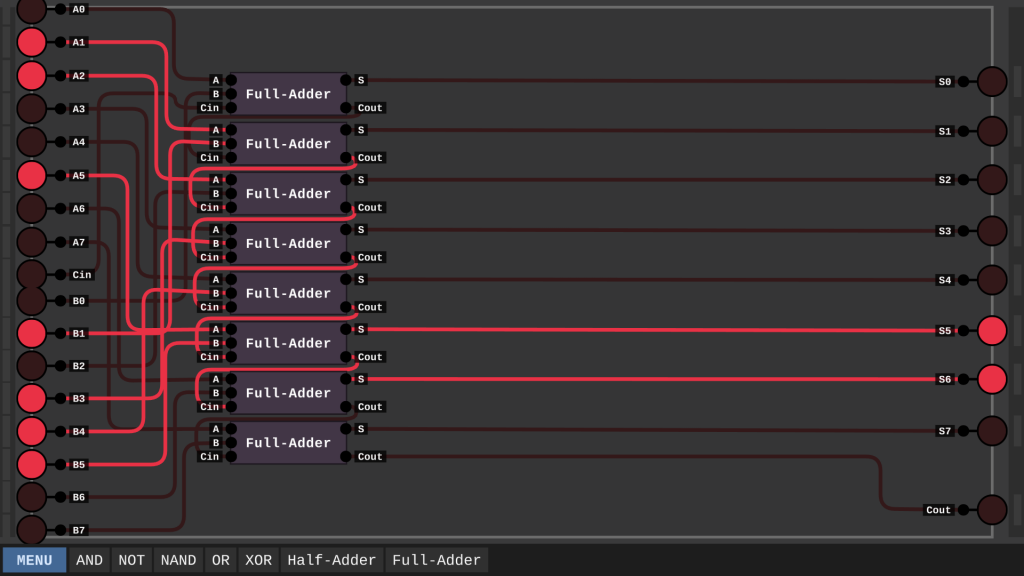
Unzwar 110000. Der erste Index von Links ist dabei S0, und so weiter.
No responses yet